Question

The state lottery board is examining the machine that randomly picks the lottery numbers. On each trial, the machine outputs a ball with one of the digits 0through 9 on it. (The ball is then replaced in the machine.) The lottery board tested the machine for 1000 trials and got the following results.Outcome 0 1 2 3 4 5 6 7 8 9Number of Trials 98 93 101 95 92 107 103 112 107 92Fill in the table below. Round your answers to the nearest thousandth,Assuming that the machine is fair, compute the theoretical probability of getting an odd(a) number.0(b) From these results, compute the experimental probability of getting an odd number.(c) Assuming that the machine fair, choose the statement below that is true:The larger the number of trials, the greater the likelihood that the experimentalprobability will be close to the theoretical probabilityThe smaller the number of trials, the greater the likelihood that the experimentalprobability will be close to the theoretical probability.The experimental probability will never be very close to the theoretical probability, nomatter the number of trials.

Answer 1

(a)0.5

(b)0.499

(c)Option A

Step-by-step explanation:

The outcome of the test is given below:

Outcome 0 1 2 3 4 5 6 7 8 9

Number of Trials 98 93 101 95 92 107 103 112 107 92

(a)The theoretical probability of getting an odd number.

The odd numbers are: 1,3,5,7,9

Number of Possible Odd Numbers =5

Total Number of Outcome = 10

Therefore, the theoretical probability of getting an odd number is:

`\begin{gathered} Theoretical\; \text{Probability}=(5)/(10) \\ =0.5 \end{gathered}`

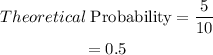
(b)Experimental probability of getting an odd number.

Total Experimental Outcomes of Odd Numbers

`\begin{gathered} =93+95+107+112+92 \\ =499 \end{gathered}`

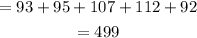
Total Number of trials =1000

Therefore, the experimental probability of getting an odd number is:

`\begin{gathered} Experimental\; \text{Probability}=(499)/(1000) \\ =0.499 \end{gathered}`

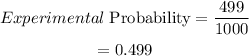
(c)

If for example, we have 2000 trials, the experimental probability of getting an odd number is:

`\begin{gathered} =(499*2)/(1000*2) \\ =0.499 \end{gathered}`

Therefore, assuming that the machine is fair, the larger the number of trials, the greater the likelihood that the experimental probability will be close to the theoretical probability.the larger the number of trials, the greater the likelihood that the experimental probability will be close to the theoretical probability.