Question

Calculate the wavelength of a photon in nn that has an energy of 2.97x10^-19J.

Answer 1

The wavelength of the photon is 0.00669 nm

Explanation:

Given information

The energy of the photon = 2.97 x 10^-19J

Let x represents the wavelength of the photon

The first thing to do is to establish the relationship between energy and photon

Recall that,

E = hf --------------- equation 1

Where

h = Planck's constant

f = frequency

`\begin{gathered} \text{Note, c = f}\lambda \\ Isolate\text{ f in the above equation} \\ f\text{ = }(c)/(\lambda)\text{ --------- equation 2} \end{gathered}`

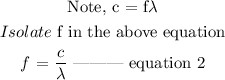
The next step is to substitute the value of f into equation 1, then, we have the below equation

`E\text{ = h}(c)/(\lambda)\text{ ------equation 3}`

Recall that,

h = 6.626 x 10^-34 J

c = 3 x 10^8 m/s

To find the wavelength, we need to substitute the above data into equation 3

`\begin{gathered} 2.97\cdot10^(-19)\text{ = }\frac{6.626\cdot10^{-34\text{ }}\text{ x 3 }\cdot10^8}{\lambda} \\ 2.97\cdot10^(-19)\text{ = }\frac{6.626\text{ x 3 }\cdot10^{-34\text{ + 8}}}{\lambda} \\ 2.97\cdot10^(-19)\text{ = }(19.878\cdot10^(-26))/(\lambda) \\ 2.97\cdot10^(-19)\text{ = }(1.9878\cdot10^(-25))/(\lambda) \\ \text{Cross multiply} \\ 1.9878\cdot10^(-25)\text{ = 2.97 }\cdot10^(-19)\text{ x }\lambda \\ \text{Isolate }\lambda \\ \lambda\text{ = }(1.9878\cdot10^(-25))/(2.97\cdot10^(-19)) \\ \lambda\text{ = }(1.9878)/(2.97)\cdot10^{-25\text{ + 19}} \\ \lambda\text{ = 0.669 }\cdot10^(-6)m \\ \lambda\text{ = 0.00669 nm} \end{gathered}`

Therefore, the wavelength of the photon is 0.00669 nm