Question

NO LINKS!!! URGENT HELP PLEASE!! Part 2

For 8 & 10, Given two sides of a triangle, find a range of possible lengths for the third side.

For 12, If a triangle has lengths of 3 ft and 54 ft, check all the possible lengths for the third side.

Answer 1

8)(28,76)

9)(1,32)

10)52,53,54,55,56

Explanation:

a+b>c>a-b

24+52>c>52-24

16+17>x>17-16

3+54>y>54-3

Answer 2

8. (28, 76)

10. (1, 33)

12. 53 ft, 55 ft

Explanation:

Triangle Inequality Theorem

The sum of the lengths of any two sides of a triangle is greater than the length of the third side.

Question 8

Let x be the length of the unknown side of the triangle.

Given two sides of a triangle are 24 ft and 52 ft then:

(a) The sum of the two given sides is greater than the third side:

`\implies 24+52 > x`

`\implies 76 > x`

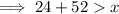
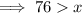
(a) The longest side is 52 ft:

`\implies 24 + x > 52`

`\implies x > 28`

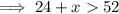
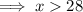
Therefore, the range of possible lengths for the third side is:

• 28 < x < 76
• Interval notation: (28, 76)

Question 10

Let x be the length of the unknown side of the triangle.

Given two sides of a triangle are 16 km and 17 km then:

(a) The sum of the two given sides is greater than the third side:

`\implies 16+17 > x`

`\implies 33 > x`

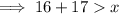
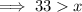
(a) The longest side is 17 km:

`\implies 16 + x > 17`

`\implies x > 1`

Therefore, the range of possible lengths for the third side is:

• 1 < x < 33
• Interval notation: (1, 33)

Question 12

Let x be the length of the unknown side of the triangle.

Given two sides of a triangle are 3 ft and 54 ft then:

(a) The sum of the two given sides is greater than the third side:

`\implies 3+54 > x`

`\implies 57 > x`

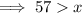
(a) The longest side is 54 ft:

`\implies 3+ x > 54`

`\implies x > 51`

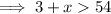
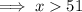
Therefore, the range of possible lengths for the third side is:

• 51 < x < 57
• Interval notation: (51, 57)

Therefore, the possible lengths for the third side of the triangle are:

• 53 ft
• 55 ft