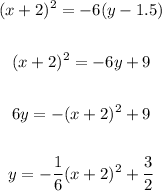Question

Find the equation of the parabola in completed square form with focus (-2,0) and directrix y=3. Use the definition of a parabola to find the equation. Then check the equation with the short cut

Answer 1

To solve the problem, it is best that we plot the given so we get an idea how the parabola looks.

The vertex of a parabola is between the directrix and the focus. Also, because we have a horizontal directrix, we know that the parabola opens downward.

Again, the vertex is right in between the directrix and the focus. So we know that the value of p is 1.5.

Using the values that we have so far, we can complete the equation. We have:

h = -2, k = 1.5, p = 1.5 direction of the parabola: opens downward

So the equation should be:

`\begin{gathered} (x-h)^2=-4p(y-k) \\ \\ (x+2)^2=-4(1.5)(y-1.5) \\ \\ (x+2)^2=-6(y-1.5) \end{gathered}`

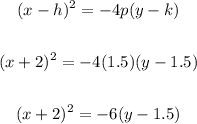
We rewrite this in the completing the square format using properties of equations.

`\begin{gathered} (x+2)^(2)=-6(y-1.5) \\ \\ (x+2)^2=-6y+9 \\ \\ 6y=-(x+2)^2+9 \\ \\ y=-(1)/(6)(x+2)^2+(3)/(2) \end{gathered}`