Question

two fifths raised to the fourth power times two fifths raised to the third power all raised to the second power

Answer 1

`\left((2)/(5)\right)^(14)\\\\`

also equal to

`(2^(14))/(5^(14))`

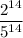
Explanation:

We have to determine

`\left[\left(\frac {2}{5}\right)^4 * \left(\frac {2}{5}\right)^3\right]^2`

When two exponents with the same base are multiplied, the resultant is the base raised to the sum of the exponents

`\textrm{Thus $x^a \cdot x^b = x^(a + b)$}\\\\In the above expression the base $(2)/(5)$ is common :\\\\Therefore\left((2)/(5)\right)^4 * \left((2)/(5)\right)^3= \left((2)/(5)\right)^(4 + 3)\\= \left((2)/(5)\right)^7\\\\`

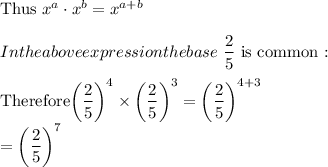
When we have an exponential term raised to another exponent, the exponents are multiplied:

`(x^a)^b = x^(a\cdot b)`

Therefore:

`\left[\left((2)/(5)\right)^7\right]^2 = \left((2)/(5)\right)^(7 \cdot 2) \\\\\\= \left((2)/(5)\right)^(14)\\\\`

We can also write this as:

`(2^(14))/(5^(14))`

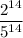
since

`\left((x)/(y)\right)^a = (x^a)/(y^a)\\`

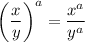
Not sure which form you want it. I am giving both