Question

9. The value, V, of a computer between 1999 and 2003 is given in the table

below. Write an equation for the line of best fit, then predict the value of
the computer in 2008.
t 1999 2000 2001 2002
V
800
720 640 572
2003
480

Answer 1

Equation of best fit line:

`\boxed{V_t = -80(t - 1999) + 800\\\\}`

`\textrm{Predicted price in 2008 =} \;\boxed{\$80}`

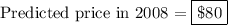
Explanation:

Let's examine the data and list the drop in price every year from 1999 to 2003

Year Drop In Price
1999 - 2000 $800 - $720 = $80

2000 - 2001 $720 - $640 = $80

2001 - 2002 $640 - $572 = $68

2002 - 2003 $572 - $480= $92

We can see that the drop in price is $80 each year for years 1999 - 2001

Between 2001 and 2003, the the drop in price for the two years was 640 - 480 = 160 so the average drop per year = 160/2 = $80

The drop in price per year is the slope of the line. The reference year is 1999 so for any year t, we have to take the difference t - 1999

The reference value is $800 since that was the value in 1999 and keeps dropping every year from that value. In function terms this is the y-intercept

A linear equation in slope-intercept form is given by

y = mx + b where m = slope, b = y-intercept

In our case we replace
y with V,
x with t-1999 where t is the actual year
m with -80(since a price drop means a negative number)
b = 800

From these observations we can infer that the equation of the best-fit line is

`\boxed{V_t = -80(t - 1999) + 800\\\\}`

For year 2008, the estimated price would be:

`V_(2008) = -80(2008-1999) + 800\\\\V_(2008) = -80 x 9 + 800\\\\V_(2008) = - 720 + 800 = \boxed{\$80}`

Additional Note

We could also use a linear regression calculator to arrive at a more accurate value for slope

The slope is -78.8 and the best-fit line would be
V = -78.8 (t - 1999) + 800

I don't know what approach your professor has suggested