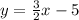Answer:
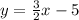
Explanation:
General format for the slope-intercept form of an equation:

where:
m = slope
c = y-intercept
 =
=
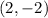
 =
=
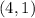
m =
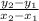
=

=

m =
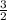
Substituting this value of m into our equation:

Substituting the coordinates of any of the two points into the above equation to solve for c:
1 =
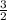 (4) + c
(4) + c
1 =
 + c
+ c
1 = 6 + c
Isolate c and make it the subject of the equation:
c =
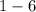
c =
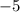
∴The slope-intercept form of the equation after substituting the calculated values of m and c: