Question

PLEASEEE HELPPP!!!!!!!! 50 POINTSSSSSS

(x+5i)(x-5i)(x-3-i)(x-3+i)

Answer 1

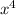`x^(4)` - 6x³ + 35x² - 150x + 250

Explanation:

note that i² = - 1

(x + 5i)(x - 5i)(x - 3 - i)(x - 3 + i) ← expand the first pair of factors using FOIL

= ( x² - 5ix + 5ix - 25i²)((x - 3) - i)((x - 3) + i) ← expand second pair using FOIL

= (x² - 25(- 1))((x - 3)²+ i(x - 3) - i(x - 3) - i²)

= (x² + 25)(x² - 6x + 9 - (- 1))

= (x² + 25)(x² - 6x + 9 + 1)

= (x² + 25)(x² - 6x + 10)

each term in the second factor is multiplied by each term in the first factor

= x²(x² - 6x + 10) + 25(x² - 6x + 10) ← distribute parenthesis

=
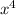`x^(4)` - 6x³ + 10x² + 25x² - 150x + 250 ← collect like terms

=
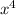`x^(4)` - 6x³ + 35x² - 150x + 250