Question

The manager at a restaurant found that the cost to produce 150 cups of coffee is $21, while the cost to produce 300 cups of coffee is $36. assume the relationship between the cost y to produce x cups of coffee is linear.

a.) write a linear equation that expresses the cost,y, in terms of the number of cups of coffee,x.
b.) how many cups of coffee are produced if the cost of production is $56?

Answer 1

`y = (1)/(10)x + 6`

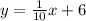
500 cups cost $56

Explanation:

Given

`x = cups`

`y = cost`

`(x_1,y_1) = (150,21)`

`(x_2,y_2) = (300,36)`

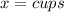
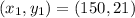
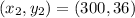
Solving (a): Linear Equation

First, we calculate the slope (m)

`m = (y_2 - y_1)/(x_2 - x_1)`

Substitute right values

`m = (36 - 21)/(300- 150)`

`m = (15)/(150)`

`m = (1)/(10)`

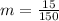
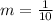
The equation is then calculated as:

`y = m(x - x_1) + y_1`

Where

`(x_1,y_1) = (150,21)`

`m = (1)/(10)`

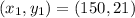
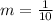
This gives:

`y = (1)/(10)(x - 150) + 21`

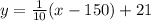
Open bracket

`y = (1)/(10)x - (1)/(10)*150 + 21`

`y = (1)/(10)x - 15 + 21`

`y = (1)/(10)x + 6`

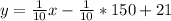
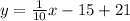
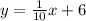
Solving (b): Cups of coffees for $56

Substitute 56 for y in
`y = (1)/(10)x + 6`

`56 = (1)/(10)x + 6`

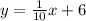
Subtract 6 from both sides

`-6+56 = (1)/(10)x + 6-6`

`50 = (1)/(10)x`

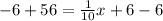
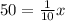
Multiply both sides by 10

`10 * 50 = (1)/(10)x * 10`

`10 * 50 = x`

`500 = x`

`x = 500`

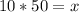
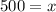
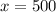
Hence: 500 cups cost $56