Question

latasha would like to invest a certain amount of money for three years and considers investing in (1) a one-year bond that pays 4 percent, followed by a two-year bond that pays the forward rate, or (2) a three-year bond that pays 8 percent in each of the next three years. latasha is considering the following investment strategies: strategy a: buy a one-year bond that pays 4 percent in year one, then buy a two-year bond that pays the two-year forward rate in years two and three. strategy b: buy a three-year bond that pays 8 percent in each of the next three years. if the two-year bond purchased one year from now pays 9 percent annually, latasha will choose . which of the following describes conditions under which latasha would be indifferent between strategy a and strategy b? the rate on the two-year bond purchased one year from now is 10.057 percent. the rate on the two-year bond purchased one year from now is 10.962 percent. the rate on the two-year bond purchased one year from now is 8.649 percent. the rate on the two-year bond purchased one year from now is 9.252 percent.

Answer 1

To find the forward rate, multiply the spot rate by the interest rate ratio and factor in the time until expiration.

The interest rate on a two-year bond purchased a year from now is 9.058%.

As a result, the forward rate equals the spot rate multiplied by (1 + domestic interest rate) / (1 + foreign interest rate).

Latasha will select Strategy B if the two-year bond purchase one year from now pays 6% annually.

This is because a 3-year return of 7% outperforms returns of 3%, 6%, and 6%.

In theory, the forward rate should equal the spot rate plus any security earnings (and any finance charges).

This principle can be seen in equity forward contracts, where the difference between forward and spot prices is based on dividends payable, less interest payable during the forward period.

Forward Rate formula

=
`[((1+S1)n^(1) )/((1+S2)n^(2) ) ]^{(1)/((n1-n2)) } -1`

Now, 3year bond rate S1 is7%

1 year bond rate S2 is 3%

3v5 Forward rate

`=(1+B5)^(3) / (1+B6)^{^{(1)/(3-1)-1 }`

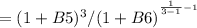
= 9.058%