Question

et X represent the full height of a certain species of tree. Assume that X has a normal distribution with a mean of 191.8 ft and a standard deviation of 4 ft. A tree of this type grows in my backyard, and it stands 182.2 feet tall. Find the probability that the height of a randomly selected tree is as tall as mine or shorter.

Answer 1

The probability that the height of a randomly selected tree is as tall as mine or shorter.

P(X≤182.2) = 0.0082

Explanation:

Step(i):-

Mean of the Population = 191.8 ft

Standard deviation of the Population = 4 ft

Let 'X' be the random variable in normal distribution

X = 182.2 feet

`Z = (x-mean)/(S.D)`

`Z = (182.2-191.8)/(4) = -2.4`

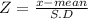
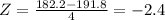
Step(ii):-

The probability that the height of a randomly selected tree is as tall as mine or shorter.

P(X≤182.2) = P( z≤ -2.4)

= 1-P(z>2.4)

= 1-(0.5 + A(2.4))

= 0.5 - A(2.4)

= 0.5 - 0.4918

= 0.0082

The probability that the height of a randomly selected tree is as tall as mine or shorter.

P(X≤182.2) = 0.0082