Answer:
a = 5 + √69
Explanation:
I am just providing another way of solving this. The answer provided by user elzny is absolutely correct and probably easier to understand. He has done a great job.
We can solve for a using the law of cosines which states that given, two sides of a triangle(say a and b) and an included angle (say C), the third side, c can be determined by the relation:
c² = a² + b² -2ab(cosC)
or
a² + b² -2ab(cosC) = c²
If we look at the triangle we see that angle C measures 60° and the two sides that include this angle are of lengths 10 and a. The third side is 12
Plugging in these values into the equation,
10² + a² - 2(10)(a)(cos 60) = 12²
100 + a² -20a(cos 60) = 144
cos 60 = 1/2
So
100 + a² - 20a (1/2) = 144
(100 - 144) + a² - 10a = 0
a² -10a -44 = 0
This is a quadratic equation which can be solved to get two values for a
The solution to this quadratic equation is done using the quadratic formula
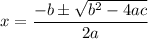
where
- a = coefficient of x² = 1 in this problem
- b = coefficient of x = -10 in this problem
- c = constant = -44
Plugging in these values,
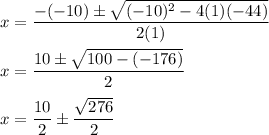
Factor 276 to get 276 = 4 x 69
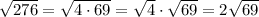
This results in
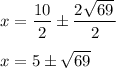
 is greater than 5 so we take only the positive component which is
is greater than 5 so we take only the positive component which is
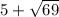
Which is the same answer as what elzny provided.
The pro of this methodology:
Direct implementation without splitting the triangle
The con:
You have to solve a quadratic equation which is not fun. But most scientific calculators can do this for you
Thanks!