Answer:
In order in which the boxes appear:
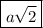
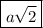
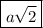
Explanation:
At any coordinate (x , y) the distance from the origin (0, 0) is computed by the distance (Pythagorean formula) as:
d =
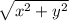
Since x = y = a for both ants, the distance is
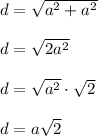
It does not matter whether both coordinates are positive or both negative since we are taking the squares of the coordinates and distance is always positive