Answer:
x > 4; r–1(x) = 4 + StartRoot StartFraction 11 Over x EndFraction EndRoot
Explanation:
We are given that
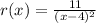
We have to find the domain of restriction on r(x) and corresponding inverse function.
Let
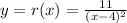
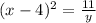
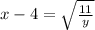
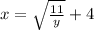
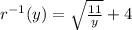
Now, replace x by y and y by x then, we get
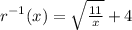
The function is not defined at x=4
But,
The inverse function defines for all positive real values.
Therefore, domain of r(x)=x>4 and inverse function
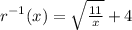
Option:
x > 4; r–1(x) = 4 + StartRoot StartFraction 11 Over x EndFraction EndRoot