We are given the following differential equation,
 , with the initial condition
, with the initial condition
 . This is a linear DE in the form,
. This is a linear DE in the form,
 , where
, where
 .
.
First, finding
 .
.
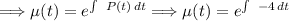
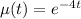
Multiply the DE by
 .
.
![\Longrightarrow(dx)/(dt)-4x=cos(5t)\Longrightarrow e^(-4t) [(dx)/(dt)-4x=cos(5t)]](https://img.qammunity.org/2024/formulas/mathematics/college/zn25admwkkeajpjo9wlb2oicb4xsnr59n4.png)
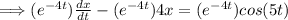
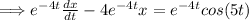
Verify that the L.H.S is a product rule of
 .
.
![\Longrightarrow (d)/(dt)[e^(-4t)x ] =(e^(-4t)*-4)x+(e^(-4t))((dx)/(dt) )](https://img.qammunity.org/2024/formulas/mathematics/college/qn3xwyj33bxnhbl46j3l4v9gbyunoq0ckk.png)
![\Longrightarrow (d)/(dt)[e^(-4t)x ] =-4e^(-4t)x+e^(-4t)(dx)/(dt)](https://img.qammunity.org/2024/formulas/mathematics/college/rmvcwts6g8hcit9w3r9oe5rjhpc1qvekz2.png)
This matches, so we can move forward by integrating both sides of the DE.
![\int\ {[e^(-4t)x ]'} \, =\int\ {e^(-4t)cos(5t)} \, dt](https://img.qammunity.org/2024/formulas/mathematics/college/bkh0vzhcqziq76bw8vf787ib6c2thfxby5.png)
The integral on the R.H.S is pretty nasty to do using integration by parts and u-sub. I will use a table of integrals.
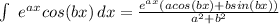
Let
 and
and
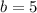
![\int\ {[e^(-4t)x ]'} \, =\int\ {e^(-4t)cos(5t)} \, dt](https://img.qammunity.org/2024/formulas/mathematics/college/bkh0vzhcqziq76bw8vf787ib6c2thfxby5.png)
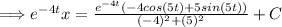
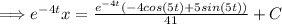
Now for the initial condition,
 .
.
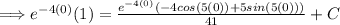
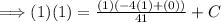
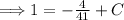
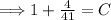
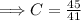
Now we have,
 , solve for x.
, solve for x.
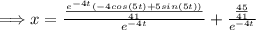
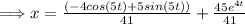
Thus, the answer to the given differential equation with an initial condition is,
 .
.