Question

Peggy invests $8, 400 at 6 1/2% interest for 10 years compounded semiannually. Find the amount of money in the account at the end of the term.

Answer 1

To find the amount of money in Peggy's account at the end of 10 years, we can use the formula for compound interest:
`A = P(1 + r/n)^{(nt),`. Plugging in the given values, we find that the final amount in Peggy's account is approximately $14,930.42.

Step-by-step explanation:

To find the amount of money in Peggy's account at the end of 10 years, we can use the formula for compound interest:
`A = P(1 + r/n)^{(nt),` where:

• A is the final amount of money in the account
• P is the principal amount invested
• r is the annual interest rate (as a decimal)
• n is the number of times interest is compounded per year
• t is the number of years

In this case, Peggy is investing $8,400 at an annual interest rate of 6 1/2% (0.065) for 10 years, with semiannual compounding (n = 2). Plugging these values into the formula, we have:

A =
`$8,400(1 + 0.065/2)^{(2*10) = $8,400(1.0325)^{20`

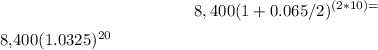
Using a calculator or a spreadsheet, we can calculate that the final amount in Peggy's account is approximately $14,930.42.

Answer 2

Answer:1200

Step-by-step explanation:1200