Answer:
- domain: all x except -3, 6
- range: all y except 0, 1/9
Explanation:
You want the domain and range of the function ...
F(x) = (x -6)/(x² -3x -18)
Domain
We can simplify the function to ...
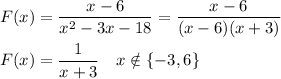
The domain is the set of x-values for which the function is defined. It is undefined where the denominator is zero. So, x=-3 and x=6 are excluded from the domain, which would otherwise be all real numbers.
Range
The range is the set of values that the function may have. Here, the function can have any y-value except 0 (the value of the horizontal asymptote), and 1/9, the location of the "hole" at x=6.
The range is all real numbers except 0 and 1/9.