Answer:
y = 2
Explanation:
The question has given us two equations with two unknown variables and told us to solve the system of equations.
To do this, there are multiple methods. The method used in this solution will involve taking any one of the variables and making it the subject of both equations and then equating the resulting equations.
Let's take the first equation:
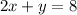 ,
,
and rearrange it to make x the subject:
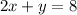
⇒
 [Subtracting y from both sides]
[Subtracting y from both sides]
⇒
 ------(i) [Dividing both sides by 2]
------(i) [Dividing both sides by 2]
Now let's take the second equation and rearrange it to also make x its subject:
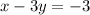
⇒
 ------(ii) [Adding 3y to both sides]
------(ii) [Adding 3y to both sides]
As both equations (i) and (ii) are equal to
 , we can say:
, we can say:
(i) = (ii)
⇒
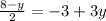
⇒
 [Multipying both sides by 2]
[Multipying both sides by 2]
⇒
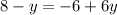
⇒
 [Subtracting 6y from both sides]
[Subtracting 6y from both sides]
⇒
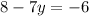
⇒
 [Subtracting 8 from both sides]
[Subtracting 8 from both sides]
⇒
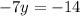
⇒
 [Dividing both dies by -7]
[Dividing both dies by -7]
⇒
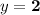
Therefore, the answer to the question is 2.
We can now easily calculate the value of x by substituting y = 2 into either equation (i) or (ii).
Substituting into (i):
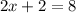
⇒
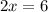
⇒
