Question

Rewrite the function in the form of f(t)=a(b)^t to determine whether it represents exponential growth or exponential decay. Identify the percent rate of change.

Answer 1

`f(t) = 4 (1.25)^(t+3) = 4 \cdot (1.25)^(3) \cdot (1.25)^(t)` using the exponent rule
`a^n\cdot a ^m = a^(n+m)` in reverse. (Using the rule to split apart the exponent.

Continuing to calculate out some values,

`f(t) = 4 \cdot (1.25)^(3) \cdot (1.25)^(t) = 4 \cdot 1.953125 \cdot (1.25)^(t) = 7.8125 \cdot (1.25)^(t)`

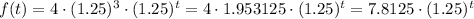
So,
`f(t) = 7.8125 \cdot (1.25)^(t)` or
`f(t) = 7.81 \cdot (1.25)^(t)` rounded to the nearest hundredth.

Since the b-value is greater than 1, this is exponential growth.

The b-value of 1.25 means that for each increase by 1 unit in the t-value, the y-value will become 125% of what it had been. The output will grown by 25%, which is your percent rate of change.

The b-value of your function is always a measurement from 100% or b=1.