Question

Given f(x)=4(x−2)^3+2, classify each statement about f^−1(x) as true or false.

Choose the answers which are correct or false.

1. The point of symmetry on f^−1(x) is (2,2).

2. The domain of f^−1(x) is (−∞,4).

3. The graphs of f^−1(x) and f(x) are reflections across the line y = x

4. f^−1(x) is not a function.

Answer 1

1. True

2. False

3. True

4. False

Explanation:

Given function:

`f(x)=4(x-2)^3+2`

1. Point of Symmetry

The point-of-symmetry of a cubic graph is its point of inflection.

To find the x-value of the point of inflection of a cubic function, differentiate the function twice:

`f'(x)=12(x-2)^2`

`f''(x)=24(x-2)`

Set the second differentiated function to zero and solve for x:

`\implies 24(x-2)=0`

`\implies x-2=0`

`\implies x=2`

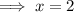
Substitute the found value of x into the original function to find the y-value of the point of inflection:

`\implies y=4(2-2)^3+2`

`\implies y=4(0)^3+2`

`\implies y=0+2`

`\implies y=2`

Therefore, the point of symmetry of the cubic function is (2, 2).

The inverse of a cubic function its reflection in the line y = x.

As the point of symmetry is (2, 2), then its reflection in the line y = x is also (2, 2).

So the point of symmetry on f⁻¹(x) is (2, 2).

2. Domain

The given function has an unrestricted domain and range.

• Domain of f(x): (-∞, ∞) → all real numbers
• Range of f(x): (-∞, ∞) → all real numbers

The domain of the inverse function is the range of the function.

The range of the inverse function is the domain of the function.

Therefore, as the domain and the range of the original function are unrestricted, so are the domain and range of the inverse function.

• Domain of f⁻¹(x): (-∞, ∞) → all real numbers
• Range of f⁻¹(x): (-∞, ∞) → all real numbers

3. Reflection across the line y = x

The inverse of a cubic function with an unrestricted domain is its reflection across the line y = x.

Therefore, the graphs of f⁻¹(x) and f(x) are reflections across the line y = x.

4. Inverse function

To find the inverse of the given function, swap x and y:

`\implies x=4(y-2)^3+2`

Rearrange to make y the subject:

`\implies x-2=4(y-2)^3`

`\implies (x-2)/(4)=(y-2)^3`

`\implies \sqrt[3]{(x-2)/(4)}=y-2`

`\implies y=\sqrt[3]{(x-2)/(4)}+2`

Replace y with f⁻¹(x):

`\implies f^(-1)(x)=\sqrt[3]{(x-2)/(4)}+2`

As we have already established, the domain and range of the inverse function are unrestricted. As each x-value has only one y-value associated with it, f⁻¹(x) is a function.