Question

ABCD is a kite, AC DB and DE = EB. Calculate the length of AC, to the nearest tenth of a centimeter.

Answer 1

7.8 cm

Explanation:

One tenth of a centimeter =
`(1)/(10) (1 cm)` = 0.1 cm . This means the answer has to be rounded to 1 decimal place.

Length of BE = Length of ED =
`(6)/(2)` = 3 cm

Focus on the triangles AED and CED. These two are right-angled triangles.

In both triangles, sides AE and CE are perpendicular sides, whose lengths will be calculated using Pythagorean Theorem:

Triangle AED:

`AD^(2) = AE^(2) + ED^(2)`

`AD^(2) - ED^(2) = AE^(2)`

`AE^(2) = 6^(2) - 3^(2)`

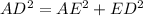
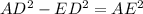
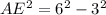
Taking square root on both sides of the equation to get rid of the square:

`AE = \sqrt{6^(2) -3^(2) }`

`AE = √(36 - 9)`

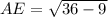
`AE = √(27)` cm

Triangle CED:

`CD^(2) = CE^(2) + ED^(2)`

`CE^(2) = CD^(2) - ED^(2)`

`CE^(2) = 4^(2) - 3^(2)`

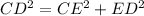
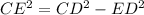
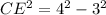
Taking square root on both sides of the equation to get rid of the square:

`CE = \sqrt{4^(2) -3^(2) }`

`CE = √(16 - 9)`

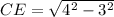
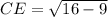
`CE = √(7)` cm

Length of AC = Length of AE + Length of EC

∴ Length of AC =
`(√(27) + √(7))` cm

= 7.841 cm

Length of AC = 7.8 cm (Rounded to the nearest tenth of a centimeter)