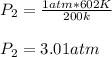Question

For a certain ideal gas, the temperature is

increased from 200 K to 602 K allowing pres-
sure, which is initially 1 atm, to vary while
the volume and number of moles of gas are
held constant. What is the new pressure?
Answer in units of atm.

Answer 1

Answer:
3.01 atm
Step-by-step explanation:
We must apply the Ideal Gas Law, which states that PV = nRT, where P is pressure, V is volume, n is the number of moles, R is the gas constant, and T is temperature, to determine the new pressure. Assuming that both the volume and the quantity of moles remain constant, we can write:

P1 / T1 = P2 / T2

where the initial pressure and temperature are P1 and T1, and the ultimate pressure and temperature are P2 and T2. Inputting the values provided yields:

P2 = P1 * T2 / T1, or 1 atm * 602 K / 200 K, or 3.01 atm.

3.01 atm is the new pressure.

Hope it helps! :)

Answer 2

Answer: The new pressure is 3.01 atm

Step-by-step explanation:

Lets used the ideal gas formula: PV = nRT

P = pressure, V = volume, n = moles, R = universal gas constant, T = temperature (in kelvin)

In this problem we are given that the change in temperature and we need to find the new pressure, when the initial pressure is 1 atm. All other variables are constant.

We can rewrite the ideal gas formula to suite this problem by saying that

P1/T1 = P2/T2

Now lets set up the equation to solve for P2

`P_(2) = (P_(1) * T_(2) )/(T_(1) )`

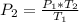
Now lets plug in the values.

P1 represents the initial pressure: 1 atm

T1 represent the inital temperature: 200k

T2 represents the final temperature: 602k

We are solving for the P2, the final (new) temperature.

`P_(2) = (1atm* 602K )/(200k )\\\\P_(2) = 3.01atm`