Question

A 8 kg Ice skater is moving at 5 m/s and is headed towards a stationary 2 kg snowman. After the two collide, the ice skater has 0 m/s of velocity and the snowman moves forward. What is the velocity of the snowman?

Answer 1

`20\; {\rm m\cdot s^(-1)}`, assuming that friction is negligible.

Step-by-step explanation:

If an object of mass
`m` moves at a velocity of
`v`, the momentum
`p` of this object would be
`p = m\, v`.

if friction is negligible, the sum of the momentum should be the same before and after the collision.

Before the collision:

• Momentum of the ice skater was
  `(8\; {\rm kg})\, (5\; {\rm m\cdot s^(-1)}) = 40\; {\rm kg \cdot m\cdot s^(-1)}`.
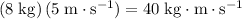• Momentum of the snowman was
  `(2\; {\rm kg})\, (0\; {\rm m\cdot s^(-1)}) = 0\; {\rm kg\cdot m\cdot s^(-1)}`.

In other words, the sum of momentum was
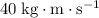`40\; {\rm kg\cdot m\cdot s^(-1)}` before the collision.

After the collision:

• Momentum of the ice skater became
  `(8\; {\rm kg})\, (0\; {\rm m\cdot s^(-1)}) = 0\; {\rm kg \cdot m\cdot s^(-1)}`.
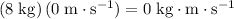• Momentum of the snowman needs to be found.

The sum of the momentum stays unchanged at
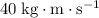`40\; {\rm kg\cdot m\cdot s^(-1)}`. Subtract the momentum of the ice skater from the sum to find the momentum of the snowman:

`40\; {\rm kg\cdot m\cdot s^(-1)} - 0\; {\rm kg\cdot m\cdot s^(-1)} = 40\; {\rm kg\cdot m\cdot s^(-1)}`.

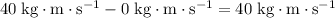Divide the momentum of the snowman by its mass to find its velocity:

`\begin{aligned}\frac{40\; {\rm kg\cdot m\cdot s^(-1)}}{2\; {\rm kg}} = 20\; {\rm m\cdot s^(-1)}\end{aligned}`.

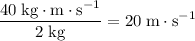In other words, the collision of the snowman would be
`20\; {\rm m\cdot s^(-1)}` after the collision.