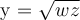Question

What expression represents the value of y?

Answer 1

Second choice:

`\mbox{\large y = √(wz)}`

Explanation:

Consider the right triangle ABC

By the Pythagorean theorem,

AB² = BC² + AC²

BC = x, AC = (w + x) and AB = v

Plug in above values
(w + z)² = v² + x² (1)

In right triangle BCD,
BC² = BD² + CD²

Plugging in values we get
x² = w² + y² (2)

In right triangle ABD
AB² = BD² + AD²
v² = y² + z² (3)

Plug in values of x² from eq (2) and v² from eq 3 into equation (1) to get

(w + z)² = y² + z² +w² + y²

Left side (w + z)² = w² + 2wz + z²

==> w² + 2wz + z² = y² + z² +w² + y²

w² and z² cancel out since they are on both sides of the equation with same sign

=> 2wz = y²+y²

2wz = 2y²

Divide by 2:

wz = y²

Switch sides:

y² = wz

`\mbox{\large y = √(wz)}`