Question

Solve algebraically, show all steps, and round 3 decimal places

Answer 1

x = 1.523

Explanation:

Given

`\quad\quad e^(x-1) = 3^(2-x)`

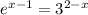
we are asked to solve for x

Take natural logs on both sides:

`\ln \left(e^(x-1)\right)=\ln \left(3^(2-x)\right)\\\\\mathrm{Apply\:log\:rule}:\quad \log _a\left(x^b\right)=b\cdot \log _a\left(x\right)}\\\\\ln \left(e^(x-1)\right)=\left(x-1\right)\ln \left(e\right)\\\\\rightarrow \left(x-1\right)\ln \left(e\right)=\ln \left(3^(2-x)\right)`substitute on left side of original eqn

`\ln \left(3^(2-x)\right)=\left(2-x\right)\ln \left(3\right)\\\\`

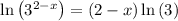
Therefore we get

`\left(x-1\right)\ln \left(e\right)=\left(2-x\right)\ln \left(3\right)`

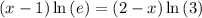
But ln(e) = 1

So we get

`x - 1 = (2-x)\;\ln(3)\\\\`

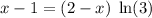
So the expression becomes

`x - 1 = (2- x) \ln(3)\\\\x - 1 = 2\ln(3) - x \ln(3)`

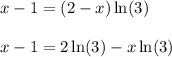
Add
`x\ln(3)` on both sides:

x + x ln(3) - 1 = 2ln(3)

Add 1 to bot sides:
x + x ln(3) = 2ln(3) + 1

x(1 + ln(3)) = 2 ln3 + 1

ln(1 + \ln(3)) = 2.09861

2ln(3) + 1 =3.1972

So we get

x(2.0986) = 3.1972

x = 3.1972/2.0986 = 1.52349

Rounded to 3 decimal places, the answer is 1.523