Answer:
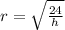 inches
inches
Explanation:
Volume of a cone =
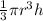
where: r = radius of cone
h = perpendicular height of the cone
Provided volume of cone = 8π cubic inches
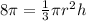
Cross multiplication is applied and 'r' is isolated:
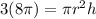

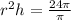
 in the numerator and denominator cancel each other out completely:
in the numerator and denominator cancel each other out completely:

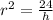
Taking the square root on both sides of the equation in order to get rid of the square:
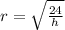 inches
inches