1 Answer

Ask a Question

Ivon · Answer 1 · 2024-11-19T04:58:20+0000

Answer:

Answer expressed in terms of pi:
$V=2304 \pi (m^(3))\\$ .

Answer rounded to the nearest whole number:
V=7238(m^(3)) .

Explanation:

1. Annotate the given data.

Given figure: Sphere.

Given dimension: diameter (d)= 24m.

2. Recall the formula.

We're trying to calculate the volume of a sphere, here's the formula for that:

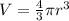
$V=(4)/(3) \pi r^(3)$

3. Use the given data (step 1) to substitute variables in the formula.

There's something worth paying a bit extra ttention in this problem, and that is the fact that we were not given a value of radius (r) to use in the formula. Instead, we were given the diameter (d), which happens to be double of the radius, by definition. Hence, to find the radius we do the following:

$d=2r\\\\ r=(d)/(2) =(24m)/(2) =12m$

Use the data in the volume formula:

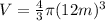
$V=(4)/(3) \pi (12m)^(3)$

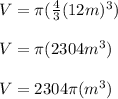
$V= \pi((4)/(3) (12m)^(3))\\ \\V= \pi(2304m^(3) )\\ \\V=2304 \pi (m^(3))\\$

4. Express the answers.

We were asked to express our answer in terms of pi. Therefore, let's isolate pi from the calculations for now:

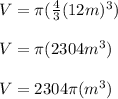
$V= \pi((4)/(3) (12m)^(3))\\ \\V= \pi(2304m^(3) )\\ \\V=2304 \pi (m^(3))\\$

Answer expressed in terms of pi:
$V=2304 \pi (m^(3))\\$ .

The problem also asks to round to the nearest whole number. So, let's go ahead and calculate an approximate value and round it to the nearest whole number:

V=7238.229474 (m^(3))

Since the first number after the dot (.) isn't 5 or greater, we may leave the whole part of the number as it is and delete the remaining decimal numbers.