Answer:
see below
Step-by-step explanation:
We are here given that ,
- maximum height of projectile= 2.4m (h)
- angle at which it is kicked = 45°
- speed of projection= ? (u)
As we know that,
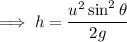
substitute the respective values,
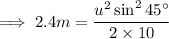
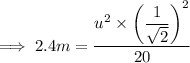
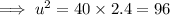
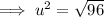
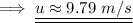
secondly we know that,
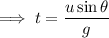
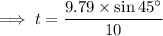
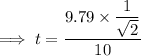

and we are done!