Question

Find the least common multiple of (x-3)^2, x^2-9, and (x+3)^3

Answer 1

`\textsf{LCM}=(x+3)^3(x-3)^2`

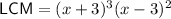
Explanation:

`\boxed{\begin{minipage}{6cm}\underline{Difference of Two Squares Formula}\\\\$a^2-b^2=\left(a+b\right)\left(a-b\right)$\\ \end{minipage}}`

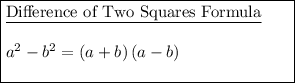
Factor x² - 9 by applying the Difference of Two Squares formula:

`\begin{aligned}\implies x^2-9&=x^2-3^2\\&=(x+3)(x-3)\end{aligned}`

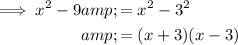
Rewrite each of the given expressions as an expansion of their factors:

`\bullet \quad (x-3)^2=(x-3)(x-3)`

`\bullet \quad x^2-9=(x+3)(x-3)`

`\bullet \quad (x+3)^3=(x+3)(x+3)(x+3)`

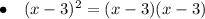
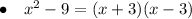
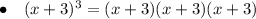
Therefore, we can see that each expression has a factor of (x - 3), (x + 3) or both (x - 3) and (x + 3).

The least common multiple (LCM) of a, b, and c is the smallest multiplier that is divisible by a, b and c.

Therefore, to find the LCM of the given expressions, multiply each factor with the highest power:

• 
  `\textsf{LCM}=(x+3)^3(x-3)^2`