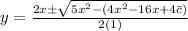Question

Verify that the indicated function y p(x) is an explicit solution of the given first-order differential equation.

(y-x)y' =y-x+ 2; y=x+2√x+3
When y = x + 2√x +3,
y'= -x+2
Thus, in terms of x,
(y - x)y' =
y-x+2=
Since the left and right hand sides of the differential equation are equal when x + 2√x + 3 is substituted for y, y = x + 2√x + 3 is a solution.
Proceed as in Example 6, by considering p simply as a function and give its domain. (Enter your answer using interval notation.)
Then by considering p as a solution of the differential equation, give at least one interval I of definition.
O(-6, -3)
O(-3,00)
(-∞, -3)
x.
(-6, 3)
O[-3, 3]
Need Help?
Read It
Watch it

Answer 1

`y=\frac{2x\pm\sqrt{5x^2-(4x^2-16x+4\bar{c})} }{2(1)}`Solve the given DE,
`(y-x)(dy)/(dx) =y-x+2`.

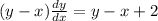Rewriting,

=>
`(y-x)(dy)/(dx) =y-x+2`

=>
`(y-x)dy =(y-x+2)dx`

=>
`-(y-x+2)dx+(y-x)dy =0`

=>
`(-y+x-2)dx+(y-x)dy =0`

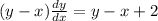
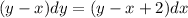
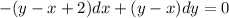
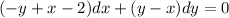
Check to see if this is an exact DE by taking the partial derivative of M with respect to y and N with respect to x.

`M=(-y+x-2)dx`

=>
`M_(y) =-1`

`N=(y-x)dy`

=>
`N_(x)=-1`

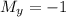
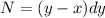
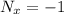
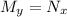`M_(y) =N_(x)`, so this is an exact DE. Now integrate M with respect to x and N with respect to y.

`\int\ ({-y+x-2)} \, dx`

=>
`-xy+(x^2)/(2)-2x`

`\int\ ({y-x)} \, dy`

=>
`=(y^2)/(2) -xy`

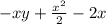
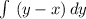
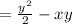
So we can say the solution to the given DE is,
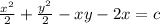`(x^2)/(2)+(y^2)/(2)-xy-2x=c`.