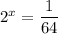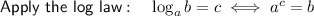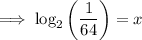Question

Can someone help me here please! thankyou​ (complete solution)​

Answer 1

1. See below.

`\textsf{2.} \quad \log_x256=(1)/(2)`

`\textsf{3.} \quad x^6=1000000`

`\textsf{4.} \quad \log_2\left((1)/(64)\right)=x`

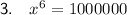
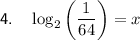
Explanation:

Question 1

Please note that this question is incorrect.

I assume the question is missing an "x" term, since log₉27 ≠ -3.

Let's assume 27 should be "x":

`\implies \log_9x=-3`

`\textsf{Apply the log law}: \quad \log_ab=c \iff b=a^c`

`\implies x=9^(-3)`

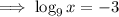
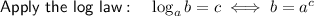
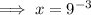
If, however, the 9 is supposed to be "x":

`\implies \log_x27=-3`

`\implies x^(-3)=27`

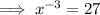
Question 2

Given exponential equation:

`√(x)=256`

`\textsf{Apply exponent rule} \quad √(a)=a^{(1)/(2)}:`

`\implies x^{(1)/(2)}=256`

`\textsf{Apply the log law}: \quad \log_ab=c \iff a^c=b`

`\implies \log_x256=(1)/(2)`

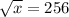
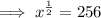
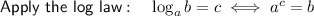
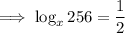
Question 3

Given logarithmic equation:

`\log_x1000000=6`

`\textsf{Apply the log law}: \quad \log_ab=c \iff a^c=b`

`\implies x^6=1000000`

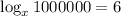
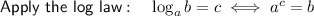
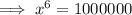
Question 4

Given exponential equation:

`2^x=(1)/(64)`

`\textsf{Apply the log law}: \quad \log_ab=c \iff a^c=b`

`\implies \log_2\left((1)/(64)\right)=x`