Answer:
The two angles are
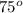 (
(
 radians) and
radians) and
 (
(
 radians)
radians)
Explanation:
Right angle =
 =
=
 radians
radians
Let x = Lesser angle
y = Greater angle
Angles in degrees:
Sum of angles in a right-angled triangle =
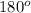

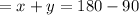

 ——(equation i)
——(equation i)
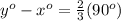
 ——(equation ii)
——(equation ii)
These two equations are linear simultaneous equations, which can be solved by substitution, elimination or graphical method:
Substitution method:
Substitute (equation i) into (equation ii) to solve for y:
Expand the brackets by applying the Distributive Law and bring all the like terms together:
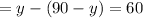


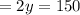
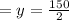
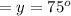
Substitute this calculated value in any of the equations to determine the value of x:
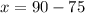
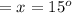
Angles in Radians:
To convert an angle measured in degrees to radians, multiply by

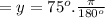
Divide both the numerator and denominator by the Highest Common Factor ‘15’:
 radians
radians
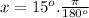
 radians
radians