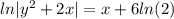Question

Solve the initial value problem 2yy, + 2 = y2 + 2x with y(0) = 8. a. To solve this, we should use the substitution u= help (formulas) With this substitution, help (formulas) help (formulas) dy Enter derivatives using prime notation (e.g., you would enter y' for >^) b. After the substitution from the previous part, we obtain the following linear differential equation in x, u, u ' . help (equations) c. The solution to the original initial value problem is described by the following equation in x, y. help (equations)

Answer 1

We have the differential equation,
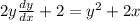`2y(dy)/(dx)+2=y^2 +2x`, solve the DE using a substitution.

Let,
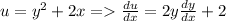`u=y^2+2x = > (du)/(dx)=2y(dy)/(dx)+2`, and make the substitutions.

=>
`2y(dy)/(dx)+2=y^2 +2x`

=>
`(du)/(dx)=u`

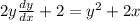
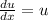
Solve the new DE using separation of variables.

=>
`(1)/(u)du=dx`

=>
`\int\ (1)/(u)du=\int\ {1} dx`

=>
`ln|u|=x+c`

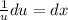
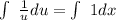
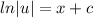
Plug
`u` back in.

=>
`ln|y^2+2x|=x+c`

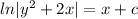
Now for the initial condition to find the arbitrary constant,
`c`.
`y(0)=8`

=>
`ln|y^2+2x|=x+c`

=>
`ln|(8)^2+2(0)|=(0)+c`

=>
`ln|(8)^2|=c`

=>
`ln|64|=c`

=>
`c=6ln(2)`

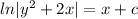
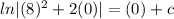
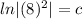
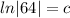
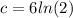
Thus the solution to the given DE with the initial condition is,

`ln|y^2+2x|=x+6ln(2)`