Question

Find the center of mass of a thin plate of constant density delta covering the given region. The region bounded by the parabola y = 3x - x^2 and the line y = -3x The center of mass is.

Answer 1

(3, -5.4)

Explanation:

You want the center of mass of a plane region of uniform density bounded by the parabola y = 3x -x² and the line y = -3x.

Bounds

The height of the region is the difference between the boundaries:

h(x) = (3x -x²) - (-3x) = 6x -x² = x(6 -x)

The height is zero at x=0 and x=6, where the factors of h(x) are zero.

Symmetry

The axis of symmetry of this height function is halfway between the zeros, at x = (0+6)/2 = 3.

Area

The area of the region is the integral of the height function between the bounds where h(x) = 0:

`\displaystyle A=\int_0^6(6x-x^2)\,dx=\left(3x^2-(x^3)/(3)\right)_0^6=36`

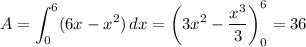
Y-dimension

The y-coordinate of the center of mass is the integral of the product of a differential of mass and its y-dimension, divided by the area.

`\displaystyle M_y=\int_0^6(((3x -x^2)+(-3x))/(2)(6x-x^2))\,dx=(1)/(2)\int_0^6(x^4-6x^3)\,dx\\\\=\left((x^5)/(10)-(3x^4)/(4)\right)_0^6=(6^4)/(20)(2\cdot6-15)=\underline{-194.4}`

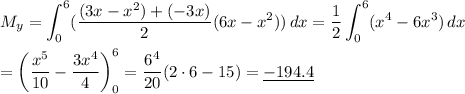
Dividing this moment by the area, we find the desired y-coordinate to be ...

`C_y=(-194.4)/(36)=-5.4`

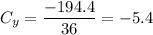
X-dimension

The x-coordinate of the center of mass is on the line of symmetry, at ...

`C_x=3`

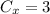
The center of mass is (3, -5.4).

__

Additional comments

Alternatively, you could take advantage of the published coordinates of the centroid of a parabolic region: 4/10 of the height above the flat edge, and on the line of symmetry. Here, the region is bounded by the line at x=3:

y = -3x = -3(3) = -9

and the parabola at x=3:

y = x(3 -x) = 3(3 -3) = 0

Then the y-coordinate of the centroid is ...

-9 +0.4(0 -(-9)) = -9 +3.6 = -5.4 . . . . . as above

centroid = (3, -5.4)

In the integral to find the y moment, we used the centroid of the differential area as the average of the upper and lower bounds of that area:

((3x -x²) + (-3x))/2 = -x²/2

Modern calculators do this integration easily, achieving full calculator precision.