Question

Please help meeeeee!!!!!!!!!!!!!

Answer 1

Answer: the ball has height 320 feet when t=0, 1 seconds

Explanation:

`Given: \ h(t)=-16t^2+16t+320\ \ \ \ h(t)=32\ feet\\\\Find\ t\geq 0\\\\`

`Solution`

`h(t)=-16t^2+16t+320\\\\320=-16t^2+16t+320\\\\0=-16t^2+16t\\\\0+16t^2=-16t^2+16t+16t^2\\\\16t^2=16t\\\\16t^2-16t=16t-16t\\\\16t^2-16t=0\\\\16(t^2-t)=0`

We divide both parts of the equation by 16:

`\displaystyle\\t^2-t=0\\\\t(t-1)=0\\\\\left \{ {{t=0} \atop {t-1=0}} \right. \ \ \ \ \ \ \Rightarrow\\\\t=0 \ \ \ \ t=1`

Answer 2

`\mbox{\large t = \boxed{1} second}`

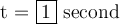
Explanation:

The function relating time and height of the ball is given as

`h(t) = -16t^2 + 16t + 320\cdots\cdots \cdots(1)`

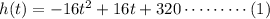
with the variables h, t as defined in the question

We are asked to find the time at which the ball reaches a height of 320 feet

Substitute 320 for h in Equation (1) and solve for t

`320 = -16t^2 + 16t + 320\\\\\textrm{Switching sides, }\\\\\\-16t^2 + 16t + 320 = 320\\\\\textrm{Subtract 320 from both sides to get}\\\\\\-16t^2 + 16t = 0`

Carry 16t to the right side:

`-16t^2 = -16t\\\\`

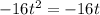
Divide both sides by -16t:

`(-16t^2)/(-16t) = (-16t)/(-16t)\\\\\implies t = 1`

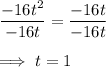
That means the ball has a height of 320 feet when t =
`\boxed{1}` second

We can check if this correct by plugging in t=1 into the original equation:

At t = 1

- 16t² + 16t + 320
= -16(1)² + 16(1) + 320

= -16 + 16 + 320

= 320

Hence t = 1 checks out