Question

The bearing from A to C is N64°W. The bearing from A to B is S82°W. The bearing from B to C is N26°E. A plane flying at 350 mph takes 1.8 hours to go from A to B. Find the distance from B to C. Round answer to the nearest mile.

Answer 1

352 miles

Step-by-step explanation:

If a plane flying at a speed of 350 mph takes 1.8 hours to go from A to B, then the distance from A to B is:

`\begin{aligned}\sf Distance&=\sf Speed * Time\\&=350 * 1.8\\&=630\; \sf miles\end{aligned}`

Draw a diagram using the given information (see attachment 1).

Calculate the internal angles of triangle ABC.

Angles on a straight line sum to 180°. Therefore:

⇒ m∠BAC = 180° - 64° - 82°

⇒ m∠BAC = 34°

According to the alternate interior angles theorem:

⇒ m∠BCA + 26° = 82°

⇒ m∠BCA = 56°

Interior angles of a triangle sum to 180°. Therefore:

⇒ m∠ABC + m∠BAC + m∠BCA = 180°

⇒ m∠ABC + 34° + 56° = 180°

⇒ m∠ABC = 90°

Add the interior angles of triangle ABC to the diagram (see attachment 2).

`\boxed{\begin{minipage}{7.6 cm}\underline{Sine Rule} \\\\$(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)$\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}`

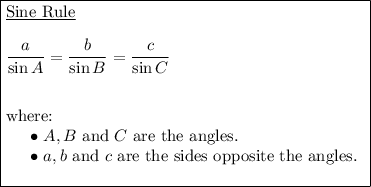
To find the distance from B to C, calculate the length of BC using the Sine Rule.

`\implies (AB)/(\sin C) =(BC)/(\sin A)`

`\implies (630)/(\sin 90^(\circ))=(BC)/(\sin 34^(\circ))`

`\implies BC=(630\sin 34^(\circ))/(\sin 90^(\circ))`

`\implies BC=352.291529...`

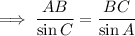
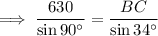
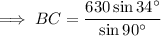
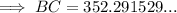
Therefore, the distance from B to C is 352 miles to the nearest mile.