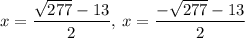Question

If using the method of completing the square to solve the quadratic equation x^2 + 13x - 27 = 0, which number would have to be added to "complete the square"?

Answer 1

Solutions are

`x=(√(277)-13)/(2),\:\:\\and\:\\x=(-√(277)-13)/(2)`

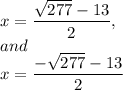
Explanation:

The given equation is x² + 13x + c = 0 with a = 1, b = 13 and c = -27

We have to transform this equation to the form
a(x + a)² + b = 0

The given equation is

`x^2\:+\:13x\:-\:27\:=\:0\\`

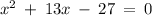
Move the constant -27 to the right side by adding 27 on both sides
==>
`x^2+13x=27`

`\mathrm{Rewrite\:in\:the\:form}\:\left(x+a\right)^2=b`:

`\left(x+a\right)^2 = x^2+2ax+a^2`

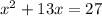
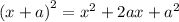
Compare

`x^2+13x \;and\; x^2+2ax+a^2`

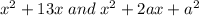
We get

`2ax = 13x`

`\mathrm{Divide\:both\:sides\:by\:}2x\\\\(2ax)/(2x)=(13x)/(2x)\\\\a=(13)/(2)`

`\mathrm{Add\:}a^2=\left((13)/(2)\right)^2\mathrm{\:to\:both\:sides}`

`x^2+13x+\left((13)/(2)\right)^2=27+\left((13)/(2)\right)^2`

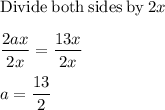
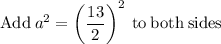
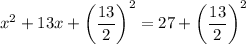
left side is

`\left(x + (13)/(2)\right)^2`

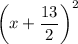
right side is

`27+\left((13)/(2)\right)^2 = 27 + (169)/(4)\\\\\\= (27 \cdot 4 + 169)/(4)\\\\= (108 + 169)/(4)\\\\= (277)/(4)`

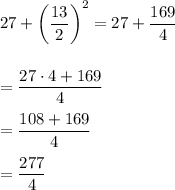
So the equation in complete the square format is

`\left(x+(13)/(2)\right)^2=(277)/(4)`

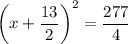
Taking square roots on both sides

`x+(13)/(2) = \pm \sqrt{(277)/(4)}\\\\`

`x = -(13)/(2) \pm \sqrt{(277)/(4)}`

`(277)/(4) =\frac{\aqrt{277}}{2}`

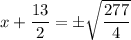
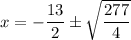
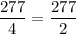
Solutions are

`x = -(13)/(2) + \sqrt{(277)/(2)} \;\\and\\\\x = -(13)/(2) - \sqrt{(277)/(2)} \;\\`

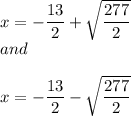
which can be rewritten as

`x=(√(277)-13)/(2),\:x=(-√(277)-13)/(2)`