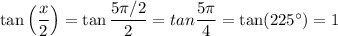Question

Which value is a solution for the equation tan x/2=-1?

A. 5 π/4
B. 7 π/4
C. 3 π/2
D. 3 π/4

Answer 1

x = 5 π/2

Doesn't fit any of the answer choices. See detailed explanation below

Explanation:

We have the equation as

`\tan\left((x)/(2)\right) = 1\\\\\mathrm{Therefore \: (x)/(2) = \tan^(-1)(1)}\\\\`

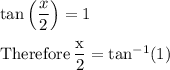
`\textrm{If $\tan\theta$ is positive, $\theta$ can either be in the first quadrant or the third quadrant}`. So possible values for θ are θ in the first quadrant and 180° + θ in the third quadrant

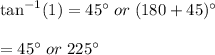
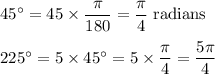
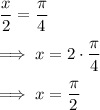
`\tan^(-1)(1)}= 45^\circ \; or \; (180 + 45)^\circ\\\\= 45^\circ \; or \; 225^\circ\\\\`

`\textrm{To convert degrees to radians multiply by }`
`(\pi)/(180)`

`\mathrm{45^\circ = 45 * (\pi)/(180) = (\pi)/(4) \;radians}\\\\225^\circ = 5* 45^\circ = 5 * (\pi)/(4) = (5\pi)/(4)\\\\`

Therefore

`(x)/(2) = (\pi)/(4) \\\\\implies x = 2\cdot (\pi)/(4)\\\\ \implies x = (\pi)/(2)`

OR

`(x)/(2) = 5(\pi)/(4) \\\\\implies x = 10\cdot (\pi)/(4)\\\\ \implies x = (5\pi)/(2)`

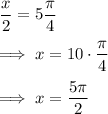
Unfortunately, none of the choices give this as an answer. But we can verify as follows

`\tan\left((x)/(2)\right)=\tan\frac{{5\pi/2}}{2} = tan(5\pi)/(4) =\tan(225^\circ ) = 1`

Answer 2

Ta n(x/2) = -1 is B. 7π/4.