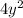Answer:
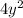
Explanation:
A = Area
w = width
l = length
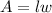
in this equation the area is
 and the length is
and the length is
 .
.
To find the equation we simply have to divide the area (
 ) by the length (
) by the length (
 ).
).
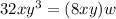
When dividing, it's important to remember two things:
- A variable divided by itself is one
- To divide a variable by the same variable with a lower exponent we have to subtract
Using these two rules, we divide the common bases (number by number, x by x, y by y):
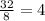
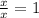
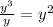
Multiplying all of them together, we find that the width is: