Question

Find the inverse of this function f(x)=(x-2)^4 (if x ≥ 2)

Answer 1

`f^(-1)(x)=\sqrt[4]{x}+2 \qquad \textsf{for $x \geq 0$}`

Explanation:

Given function:

`f(x)=(x-2)^4`

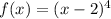
The domain of the given function is restricted:

• {x : x ≥ 2}

Therefore, the range of the given function is also restricted:

• {f(x) : f(x) ≥ 0}

To find the inverse of a function, swap x and y:

`\implies x=(y-2)^4`

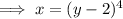
Rearrange the equation to make y the subject:

`\implies \sqrt[4]{x}=y-2`

`\implies y=\sqrt[4]{x}+2`

Replace y with f⁻¹(x):

`\implies f^(-1)(x)=\sqrt[4]{x}+2`

The domain of the inverse of a function is the same as the range of the original function. Therefore, the domain of the inverse function is restricted to {x : x ≥ 0}.

Therefore, the inverse of the given function is:

`f^(-1)(x)=\sqrt[4]{x}+2 \qquad \textsf{for $x \geq 0$}`