Find the midpoints of each of the sides of a triangle ABC, where A is (1, 1), B is (5,5) and C is (11,2).

Question

asked May 20, 2024 85.9k views

1 Answer

Damon Abdiel · Answer 1 · 2024-05-25T10:30:59+0000

Answer:

Midpoint AB

$(3, 3)\\$

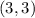
Midpoint BC

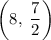
$\left(8, \; (7)/(2)\right)$

Midpoint AC

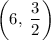
$\left(6, \; (3)/(2)\right)$

Explanation:

The midpoint (x, y) between any two points(x1, y1) and (x2, y2) can be calculated using

x = (x1 + x2)/2
y = (y1 + y2)/2

Given
A(1, 1)
B(5, 5)
C(11, 2)

Midpoint of AB

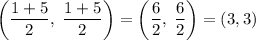
$\left((1+5)/(2), \;(1+5)/(2)\right) = \left((6)/(2), \;(6)/(2)\right) = (3, 3)$

Midpoint of BC :

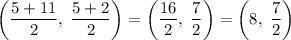
$\left((5+11)/(2), \;(5+2)/(2)\right) = \left((16)/(2), \;(7)/(2)\right) = \left(8, \; (7)/(2)\right)$

Midpoint of AC:

$\left((1+11)/(2), \;(1+2)/(2)\right) = \left((12)/(2), \;(3)/(2)\right) = \left(6, \; (3)/(2)\right)$