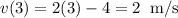Question

Can anyone assist me with this, many thanks.

Answer 1

1.a) x = g(2)

1.b) See below

2.a) See below

2.b) α = 60°

3.a) 2 + h

3.b) 2

4.a) Interval [3, 4] = 3 m/s

Interval [3, 3.1] = 2.1 m/s

4.b) 2 m/s

Explanation:

Question 1

Part (a)

Given function f(x):

`f(x)=(x)/(x-2)`

If the range of f is (-∞, 1) U (1, ∞), then a value of y in the range of f is y=2.

Set the function equal to the value of y and solve for x:

`\begin{aligned}y=2 \implies (x)/(x-2)&=2\\x&=2(x-2)\\x&=2x-4\\-x&=-4\\x&=4\end{aligned}`

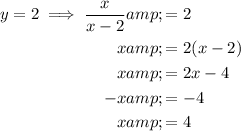
The solution written as a function x = g(y) is:

• x = g(2)

Part (b)

Given function g(y):

`g(y)=(2y)/(y-1)`

Verify that g is the inverse function of f by calculating g(f(x)):

`\begin{aligned}\implies g(f(x)) &=(2f(x))/(f(x)-1)\\\\&=(2\left((x)/(x-2)\right))/(\left((x)/(x-2)\right)-1)\\\\&=(2\left((x)/(x-2)\right))/(\left((x-(x-2))/(x-2)\right))\\\\&=(\left((2x)/(x-2)\right))/(\left((2)/(x-2)\right))\\\\&=(2x)/(2)\\\\&=x \quad (\text{for all $x\\eq 2$})\end{aligned}`

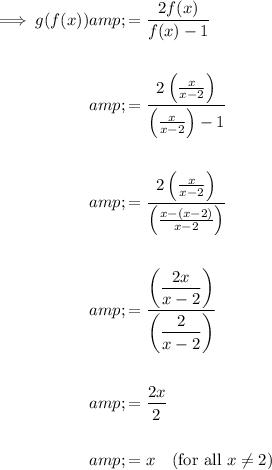
Similarly, calculate f(g(y)):

`\begin{aligned}\implies f(g(y))&=(g(y))/(g(y)-2)\\\\&=(\left((2y)/(y-1)\right))/(\left((2y)/(y-1)\right)-2)\\\\&=(\left((2y)/(y-1)\right))/(\left((2y-2(y-1))/(y-1)\right))\\\\&=(\left((2y)/(y-1)\right))/(\left((2)/(y-1)\right))\\\\&=(2y)/(2)\\\\&=y \quad \text{(for all $y \\eq 1$)}\end{aligned}`

Hence verifying that g is the inverse function of f.

Question 2

`\boxed{\begin{minipage}{5 cm}\underline{Trigonometric Identities}\\\\$\tan x=(\sin x)/(\cos x)$\\\\\\$\cos \left(\arctan \left(x\right)\right)=(1)/(√(1+x^2))$\\\\\\$\sin\left(\arctan \left(x\right)\right)=(x)/(√(1+x^2))$\\\end{minipage}}`

Part (a)

If y = arctan(x) then tan(y) = x.

Use the trigonometric identities to express sin(y) and cos(y) in terms of x.

`\boxed{\begin{aligned}\tan(y) &= x\\\implies (\sin y)/(\cos y)&=x\\\sin y&=x \cos y\\ \sin y&=x \cos (\arctan x)\\ \sin y&=(x)/(√(1+x^2))\end{aligned}}`

`\boxed{\begin{aligned}\tan(y) &= x\\\\\implies (\sin y)/(\cos y)&=x\\\\(\sin y)/(x)&= \cos y\\\\ \cos y&=(\sin(\arctan x))/(x)\\\\ \cos y&=((x)/(√(1+x^2)))/(x)\\\\\cos y&=(x)/(√(x^2+1)x)\\\\\cos y&=(1)/(√(x^2+1))\end{aligned}}`

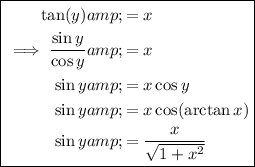
Part (b)

Given linear equation:

`y=√(3)x+1`

As the slope of a linear equation y = mx + b is m, then the slope (m) of the given line is √3.

If m = tan(α) then:

`\begin{aligned}\implies m&=√(3)\\\tan (\alpha)&=√(3)\\\alpha&=\arctan √(3)\\\alpha&=60^(\circ)+180^(\circ)n\\\end{aligned}`

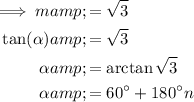
If α is the angle the line forms with the x-axis, then α = 60°.

Question 3

Given function:

`f(x)=x^2-1`

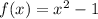
Part (a)

`\begin{aligned}(f(1+h)-f(1))/(h) &=(((1+h)^2-1)-(1^2-1))/(h)\\\\&=((1+2h+h^2-1)-0)/(h)\\\\&=(2h+h^2)/(h)\\\\&=2+h\end{aligned}`

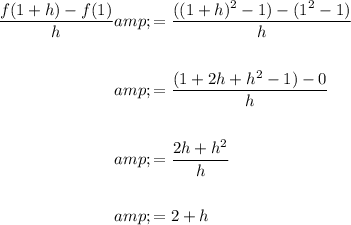
Part (b)

Part a used differentiating from first principles to find the gradient of f(x) at x = 1. As h gets smaller, the gradient of the straight line gets closer and closer to the gradient of the curve. Therefore, as h gets close to zero, (2 + h) gets close to 2. Therefore, the slope of the tangent line to the graph of f(x) at the point where x = 1 is 2.

Question 4

A particle is moving on the x-axis and its position at time is given by

`x(t)=t^2-4t+3`

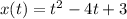
Evaluate the position of the particle at t = 3, t = 4 and t = 3.1:

`x(3)=3^2-4(3)+3=0`

`x(4)=4^2-4(4)+3=3`

`x(3.1)=(3.1)^2-4(3.1)+3=0.21`

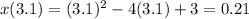
Average velocity formula

`\overline{v}=(s(t_2)-s(t_1))/(t_2-t_1)`

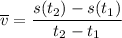
Therefore, the average velocity of this particle over the interval [3, 4]:

`\overline{v}=(x(4)-x(3))/(4-3)=(3-0)/(1)=3\;\; \rm m/s`

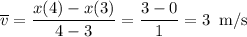
The average velocity over the interval [3, 3.1] is:

`\overline{v}=(x(3.1)-x(3))/(3.1-3)=(0.21-0)/(0.1)=2.1\;\; \rm m/s`

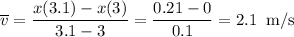
Part (b)

To find an equation for velocity, differentiate the given equation for displacement:

`v(t)=\frac{\text{d}x}{\text{d}t}=2t-4`

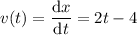
To calculate the instantaneous velocity of the particle at time t = 3, substitute t = 3 into the equation for velocity:

`v(3)=2(3)-4=2\;\; \rm m/s`