Question

Write a
linear function f with f (5) = -1 and
f (0) = -5.
f(x) =

Answer 1

`\huge\begin{array}{ccc}f(x)=(4)/(5)x-5\end{array}`

The linear function.

We have:

`f(5)=-1\\\\f(0)=-5`

therefore we have two points on the line:

`(5,-1),\ (0,-5)`

Use the two points-slope formula:

`A(x_a,\ y_A),\ B(x_B,\ y_B)\\\\y-y_A=(y_B-y_A)/(x_B-x_A)(x-x_A)`

Substitute:

`(5,-1)\to x_A=5,\ y_A=-1\\(0,-5)\to x_B=0,\ y_B=-5`

`y-(-1)=(-5-(-1))/(0-5)(x-5)\\\\y+1=(-5+1)/(-5)(x-5)\\\\y+1=(-4)/(-5)(x-5)\\\\y+1=(4)/(5)(x-5)\\\\y+1=(4)/(5)x-4\\\\y+1-1=(4)/(5)x-4-1\\\\\boxed{y=(4)/(5)x-5}`

Answer 2

f(x) = 0.8x - 5

Explanation:

the equation of a linear function is of the form

f(x) = ax + b

to find a and b use the given points

f(5) = - 1 ⇒ (5, - 1)

f(0) = - 5 ⇒ (0, - 5 )

substituting into the standard form , (0, - 5 )

- 5 = a(0) + b

- 5 = b

then

f(x) = ax - 5

substitute the other point (5, - 1 )

- 1 = 5a - 5 ( add 5 to both sides )

4 = 5a ( divide both sides by 5 )

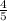`(4)/(5)` = a

f(x) =
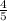`(4)/(5)` x - 5

or

f(x) = 0.8x - 5