Answer:
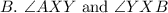
Skills needed: Angle Geometry
Explanation:
1) We are given a diagram and are asked about complementary angles.
We must fully understand this term prior to solving this problem.
---> Complementary angles are angles that add up to a measure of 90 degrees. Essentially, two complementary angles make up a right angle.
2) Let's find all right angles in the diagram.
-->
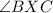 is the only marked right angle, but there are 3 others.
is the only marked right angle, but there are 3 others.
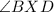 is a straight angle, since
is a straight angle, since
 is a straight line.
is a straight line.
---> A straight angle has a measure of
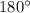 .
.
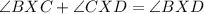 as seen in the diagram.
as seen in the diagram.
Given
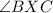 is 90 degrees (since it's a right angle), and
is 90 degrees (since it's a right angle), and
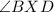 is 180 degrees (since it's a straight angle), we can solve for
is 180 degrees (since it's a straight angle), we can solve for
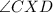
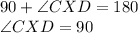
This means ANGLE CXD is a right angle.
We can do this process 2 more times. Using the fact that
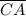 is a straight line (so
is a straight line (so
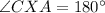 ), we can determine that
), we can determine that
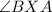 and
and
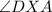 are both right angles.
are both right angles.
3) Now let's see if there are any two angles that combine to make a right angle.
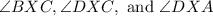 all are not split.
all are not split.
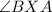 however, is split into two angles (
however, is split into two angles (
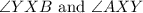
These two angles would be complementary as they make up a right angle.
 is the answer.
is the answer.