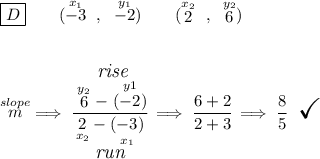first off let's find the slope of M
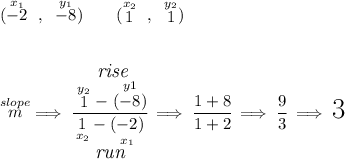
now, any line that intersects M will have a different slope than M, and since they're both lines and going to infinity, they will intersect at some point, so let's check those points for their slope, who is different than M's
![\boxed{A}\qquad (\stackrel{x_1}{0}~,~\stackrel{y_1}{2})\qquad (\stackrel{x_2}{1}~,~\stackrel{y_2}{5}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{5}-\stackrel{y1}{2}}}{\underset{\textit{\large run}} {\underset{x_2}{1}-\underset{x_1}{0}}} \implies \cfrac{ 3 }{ 1 } \implies 3 ~~ \bigotimes \\\\[-0.35em] ~\dotfill](https://img.qammunity.org/2024/formulas/mathematics/college/rhdxlnpe2npjjqfwu38fd232j2e1vn67kn.png)
![\boxed{B}\qquad (\stackrel{x_1}{-2}~,~\stackrel{y_1}{-1})\qquad (\stackrel{x_2}{3}~,~\stackrel{y_2}{14}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{14}-\stackrel{y1}{(-1)}}}{\underset{\textit{\large run}} {\underset{x_2}{3}-\underset{x_1}{(-2)}}} \implies \cfrac{14 +1}{3 +2} \implies \cfrac{ 15 }{ 5 } \implies 3 ~~ \bigotimes \\\\[-0.35em] ~\dotfill](https://img.qammunity.org/2024/formulas/mathematics/college/9bg178aywdfxjm5lfhdkgm207l8kiabfao.png)
![\boxed{C}\qquad (\stackrel{x_1}{2}~,~\stackrel{y_1}{1})\qquad (\stackrel{x_2}{-5}~,~\stackrel{y_2}{-20}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{-20}-\stackrel{y1}{1}}}{\underset{\textit{\large run}} {\underset{x_2}{-5}-\underset{x_1}{2}}} \implies \cfrac{ -21 }{ -7 } \implies 3 ~~ \bigotimes \\\\[-0.35em] ~\dotfill](https://img.qammunity.org/2024/formulas/mathematics/college/738plqkan73ca7h7isubcfwsjfcv81mzs6.png)