Answer:
P(A) = 11/18
P(B) = 5/18
P(C) = 1/9
=====================================================
Step-by-step explanation:
Check out the diagram below. I have marked your given diagram with fractions. The red fractions 1/3, 1/3, and 1/3 are probabilities that correspond to picking the left-most set of 3 branches. Each has 1/3 chance of randomly being selected. This assumes any of the branches are equally likely.
The blue fractions 1/2 and 1/3 are the probabilities for the next set of sub-branches. For instance, the upper pair of branches each have probability 1/2 of being randomly selected, since we have two of them.
The green fractions are the result of multiplying the red and blue fractions along a particular pathway. Eg: The upper-most pathway has (1/3)*(1/2) = 1/6
---------------
The diagram below shows that:
- The green fractions 1/6, 1/9, and 1/3 correspond to room A. So 1/6+1/9+1/3 = 3/18+2/18+6/18 = 11/8 is the probability of landing in room A. Therefore, P(A) = 11/18
- The green fractions 1/6 and 1/9 correspond to room B. We have P(B) = 1/6+1/9 = 3/18+2/18 = 5/18 as the probability of ending in room B.
- Lastly, P(C) = 1/9 as there's only one fraction in green corresponding to room C.
In summary
- P(A) = 11/18
- P(B) = 5/18
- P(C) = 1/9
Side notes:
- The probabilities P(A), P(B), and P(C) add to 1.
- Each probability is in the interval
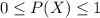
- 1/9 = 2/18