Question

Which of the following is the vertex of y=-3x^2-18x-24

Answer 1

vertex is at (-3, 3)

No choices provided; can't help you there

Explanation:

General equation of a parabola isy = ax² + bx + c

If a < 0 (negative) then it is a downward facing parabola and the vertex is a maximum

If a > 0 then it is an upward facing parabola and the vertex is a minimum

Given parabola is
y = -3x² - 18x -24

and comparing to the general equation we get a = -3, b = -18 and c = -24

So the vertex is a maximum

The x-coordinate of the vertex is given by

`x_v =- (b)/(2a)\\\\`

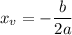
Plugging in values of a = -3 and b = -18 we get

`x_v=-(\left(-18\right))/(2\left(-3\right))\\\\\rightarrow -(-18)/(-6) = -(3) = -3\\\\`

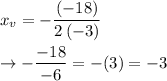
To find
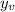`y_v`, the y-coordinate of the vertex, plug this value of
`x_v` into the parabola equation and solve for y

`y_v=-3\left(-3\right)^2-18\left(-3\right)-24\\\\y_v = -3(9) +54 -24\\\\y_v = -27 + 54 - 24\\\\y_v = 3\\\\`

So the vertex is at (-3, 3)

No choices provided so unable to help in that regard