Question

asked Dec 12, 2024 170k views

1 Answer

Grant · Answer 1 · 2024-12-18T05:04:25+0000

Answer:

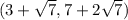
(3+√(7),7+2√(7))

(3-√(7),7-2√(7))

Explanation:

Given equations:

$\begin{cases}y=2x+1\\y=x^2-4x+3\end{cases}$

Substitute the second equation into the first equation:

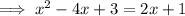
$\implies x^2-4x+3=2x+1$

Rearrange so that the terms in x are on the left side of the equation and the constants are on the right:

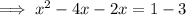
$\implies x^2-4x-2x=1-3$

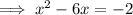
$\implies x^2-6x=-2$

Add the square of half the coefficient of the term in x to both sides:

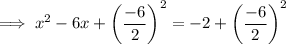
$\implies x^2-6x+\left((-6)/(2)\right)^2=-2+\left((-6)/(2)\right)^2$

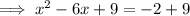
$\implies x^2-6x+9=-2+9$

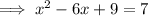
$\implies x^2-6x+9=7$

Factor the perfect square trinomial on the left side of the equation:

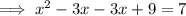
$\implies x^2-3x-3x+9=7$

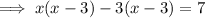
$\implies x(x-3)-3(x-3)=7$

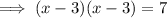
$\implies (x-3)(x-3)=7$

$\implies (x-3)^2=7$

Square root both sides of the equation:

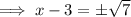
$\implies x-3=\pm √(7)$

Add 3 to both sides of the equation:

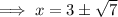
$\implies x=3\pm√(7)$

To find the y-values, substitute the found x-values into the first equation:

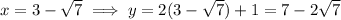
$x=3+√(7)\implies y=2(3+√(7))+1=7+2√(7)$

$x=3-√(7)\implies y=2(3-√(7))+1=7-2√(7)$

Therefore, the solutions to the system of equations are:

Please log in or register to add a comment.