Question

What can we say about the relationship between the correlation r and the slope b of the least-squares line for the same set of data? O both r and b always have values between -1 and 1 O b is always larger than r O r is always larger than b O the slope b is always equal to the square of the correlation O r and b are both positive or both negative

Answer 1

Answer: r and b are both positive or both negative

Reason:

The correlation coefficient r is between -1 and 1

`-1 \le r \le 1`

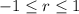
If r = -1, then we have perfect negative correlation. All points are on the same straight line that goes downhill as you move to the right. This slope is negative. If -1 < r < 0, then we still have negative slope but the points aren't all on the same line.

If r = 1, then the slope is positive. The regression line moves upward as you move to the right. All points are on this line. If 0 < r < 1, then the points aren't on the same line but we have a positive slope.

If r = 0, then we have no linear correlation at all. Either the points are randomly scattered or they fall on a curve (eg: parabola).

In short:

• negative correlation goes with negative slope
• positive correlation goes with positive slope