Question

Write an equation (In the form of g(m) = P(1+r)^m) for the exponential function from the table below.

Answer 1

Equation is

`\mbox {\large \boxed{g(m) = 4.411 (0.94988)^m}}`

Explanation:

We have to translate the information in the table as an equation of the form

`g(m) = P(1 + r)^m\cdots \cdots(1)`

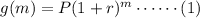
Let's take the date from the table

For m = 1, g(m) = 4.19

Substituting these values in equation (1) we get:

`g(1) = P(1 + r)^1`

`4.19 = P(1 + r)^1`

`P(1 + r)^1 = 4.19 \; \textrm{ (by switching sides)}`

`P(1+r) = 4.19\; \cdots \cdots (2)\\\textrm{ (an expression raised to the power 1 is the expression itself)}`

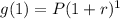
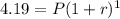
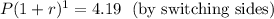
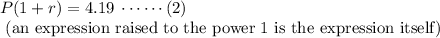
For the next entry in the table, m = 2, g(m) = 3.98

Plugging into (1)

`3.98 = P(1 + r)^2 \cdots\cdots(3)`
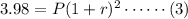
or

`P(1 + r)^2 = 3.98`

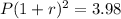
Divide equation (3) by equation (2)

`(P(1+r)^2)/(P(1+r) = (3.98)/(4.19)`

`\textrm{The P terms cancel and } ((1 + r)^2)/((1+r)) = 1 + r`

==>
`1 + r = (3.98)/(4.19)\\\\1 + r = 0.94988\\\\`

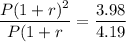
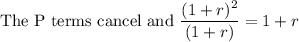
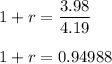
Plugging this value of 1 + r into equation (2):

`P( 0.94988) = 4.19\\\\P = (4.19)/(0.94988)\\\\P = 4.411\\\\`

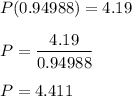
So the equation is

`g(m) = 4.411 (0.94988)^m`

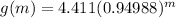
We can verify this is correct for m = 2, 3 and 4

`m\quad\quad g(m) = 4.411(0.94988)^m\\\------------------\\2\quad\quad 4.411(0.94988)^2 = 3.97992 \approx 3.98\\\\3\quad\quad 4.411(0.94988)^3 = 3.78044 \approx 3.78\\\\3\quad\quad 4.411(0.94988)^4 = 3.59097 \approx 3.59\\\\`